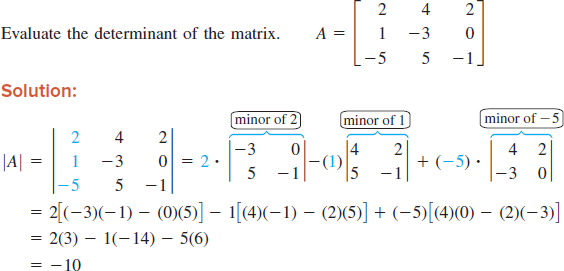
The area of the triangle is 12.5 square units. And when we apply that to the area formula, we obtain ½ (25) = 12.5. Now use the diagonal method and add the bottom products and subtract the top products: -8 + (-4) + 18 – 8 – (-24) –(-3) = 25. The area of a triangle whose vertices have coordinates (a, b), (c, d), (e, f) can be found by using the formula:Įxample: Find the area of the triangle whose vertices have coordinates (-4, -1), (3, 2), (4, 6).Īssign values to a, b, c, d, e, and f in the above formula: a = -4, b = -1, c = 3, d = 2, e = 4, f = 6 The value is:aei + bfg + cdh – gec – hfa – idbĭeterminants are utilized to calculate the area of a triangle when you know the coordinates of the three vertices.To find the value of the determinant, add the products in the first set of diagonals, and then subtract the products from the second set of diagonals.
STEP 3: Now draw a diagonal from each element in the bottom row upwards and deduce the product of the numbers on each. STEP 2: Draw a diagonal from each element in the top row downwards and deduce the product of the numbers on each diagonal. STEP 1: Write the first two columns on the right side of the determinant as shown below. Its definition is unfortunately not very intuitive. There is another simpler method utilizing diagonals for evaluating a third-order determinant. The determinant of a square matrix is a number that provides a lot of useful information about the matrix. If A is (n x n), its determinant may be defined in terms of the order (n-1) or less. If A = is a single element (1×1), then the determinant is defined as the value of the element For each square matrix A, there is a unit scalar value known as the determinant of A, denoted by det A or |A|.If det(A)=0, the matrix is said to be singular.The determinant contains the same elements as the matrix which are enclosed between vertical bars instead of brackets in a scalar equation. The Determinants of Matrix in Matrices is Represented ByĤ.To compute the inverse of a matrix, the determinant is required. The determinant is implemented in the Wolfram Language as Det m. Note that the notation may be more convenient when indicating the absolute value of a determinant, i.e., instead of. According to the Determinant Properties, the Value of Determinant Equals to Zero if Row isĢ. The determinant of a matrix, (5) is commonly denoted, , or in component notation as, , or (Muir 1960, p. If you cant see the pattern yet, this is how it looks when the elements of. This is the beauty of Maths, it never gets old!ġ. The determinant of matrix A is equal to the difference of the product of elements a. Thus, it is a very old concept and continues to hold such a high level of importance to this date. He devised it as a way of determining solutions for the quadratic equations. The Determinants are calculated byĭet \ = R.H.Sįun Fact: You might find it very interesting to know that Determinants were introduced by the great Mathematician and physicist Gauss in his book Disquisitiones arithmeticae while talking about quadratic equations in 1801. The Determinant of a square Matrix is a value ascertained by the elements of a Matrix. If X’ is a Matrix made by interchanging the positions of two rows, then det (X’) = -det (x) There is a change of sign under row swap. We will see that determinant of triangular. Invariance under row operations if X’ is a Matrix formed by summing up the multiple of any row to another row, then det (X) = det (X’). We will define determinant of SQUARE matrices, inductively, using the definition of Minors and cofactors. Invariance under transpose det (X) = det (X t ). 
Multiplicativity det (XY) = det (X) det (Y) det(An)det(A)n A very important property of the determinant of a matrix, is that it is a so called multiplicative function. The Determinant is considered an important function as it satisfies some additional properties of Determinants that are derived from the following conditions. When the determinant of a matrix is zero, the volume of the region with sides given by its columns or rows is zero, which means the matrix considered as a.
The determinant of a matrix with any two identical rows or columns is zero, i.e. The Determinants and its properties are useful as they enable us to obtain the same outcomes with distinct and simpler configurations of elements. Determinant of a Matrix The determinant of a matrix and its own transpose are always equal, i.e., Interchanging any two rows or columns of a matrix would change the sign of its determinant, i.e. The Determinants of a Matrix say K is represented as det (K) or, |K| or det K. In Linear Algebra, a Determinant is a unique number that can be ascertained from a square Matrix.
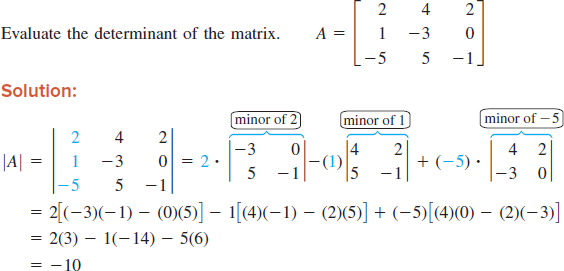
0 kommentar(er)
